How To Find Intervals On A Graph

All Calculus one Resources

On what intervals does f(x) = (1/three)x³ + ii.5xⁱⁱ– 14x + 25 increment?

Possible Answers:

(–∞, –seven), (–seven, 2), and (ii, ∞)

(–7, 2), and  (2, ∞)

(–∞, –7) and (2, ∞)

(2, ∞)

(–∞, –seven)

Correct answer:

(–∞, –7) and (2, ∞)

Explanation:

We will utilise the tangent line slope to ascertain the increasing / decreasing of f(ten). To this end, let us begin by taking the get-go derivative of f(x):

f'(x) = 10² + 5x – 14

Solve for the potential relative maxima and minima by setting f'(x) to 0 and solving:

x² + 5x – xiv = 0; (x – two)(10 + vii) = 0

Potential relative maxima / minima: x = 2, x = –seven

We must examination the following intervals: (–∞, –7), (–7, two), (2, ∞)

f'(–10) = 100 – 50 – 14 = 36

f'(0) = –fourteen

f'(10) = 100 + 50 – xiv = 136

Therefore, the equation increases on (–∞, –7) and (2, ∞)

Find the interval(due south) where the following part is increasing. Graph to double check your respond.

Possible Answers:

Never

Always

Correct answer:

Caption:

To find when a function is increasing, you must first take the derivative, then prepare information technology equal to 0, then find betwixt which zero values the office is positive.

First, take the derivative:

Prepare equal to 0 and solve:

Now test values on all sides of these to discover when the function is positive, and therefore increasing. I will test the values of -6, 0, and ii.

Since the values that are positive is when x=-6 and 2, the interval is increasing on the intervals that include these values. Therefore, our reply is:

Notice the interval(s) where the following function is increasing. Graph to double bank check your answer.

Possible Answers:

Always

Never

Correct respond:

Explanation:

To find when a function is increasing, you must first take the derivative, then ready it equal to 0, and then detect betwixt which zero values the function is positive.

First, take the derivative:

Set equal to 0 and solve:

Now test values on all sides of these to detect when the function is positive, and therefore increasing. I will test the values of 0, 2, and 10.

Since the value that is positive is when x=0 and 10, the interval is increasing in both of those intervals. Therefore, our answer is:

Is  increasing or decreasing on the interval ?

Possible Answers:

Increasing. on the interval.

Increasing. on the interval.

Cannot be determined from the data provided

Decreasing. on the interval.

Decreasing. on the interval.

Correct reply:

Increasing. on the interval.

Explanation:

To notice increasing and decreasing intervals, we need to find where our first derivative is greater than or less than cipher. If our first derivative is positive, our original function is increasing and if g'(10) is negative, yard(x) is decreasing.

Begin with:

If nosotros plug in any number from 3 to vi, we get a positve number for thousand'(x), So, this function must exist increasing on the interval {3,half dozen}, because one thousand'(x) is positive.

Is  increasing or decreasing on the interval ?

Possible Answers:

Increasing, considering  is positive.

Decreasing, because  is positive.

Decreasing, considering  is negative.

Increasing, considering is negative.

 is neither increasing nor decreasing on the given interval.

Right respond:

Increasing, because  is positive.

Caption:

To find out if a function is increasing or decreasing, we demand to find if the first derivative is positive or negative on the given interval.

So starting with:

Nosotros get:

 using the Ability Rule .

Find the function on each stop of the interval.

And so the first derivative is positive on the whole interval, thus 1000(t) is increasing on the interval.

Is the following function increasing or decreasing on the interval ?

Possible Answers:

Decreasing, because  is positive on the given interval.

The function is neither increasing nor decreasing on the interval.

Increasing, because  is positive on the given interval.

Decreasing, considering  is negative on the given interval.

Increasing, because  is negative on the given interval.

Right answer:

Increasing, considering  is positive on the given interval.

Caption:

A office is increasing on an interval if for every point on that interval the first derivative is positive.

So we need to find the first derivative and so plug in the endpoints of our interval.

Find the outset derivative by using the Power Rule

Plug in the endpoints and evaluate the role.

Both are positive, so our function is increasing on the given interval.

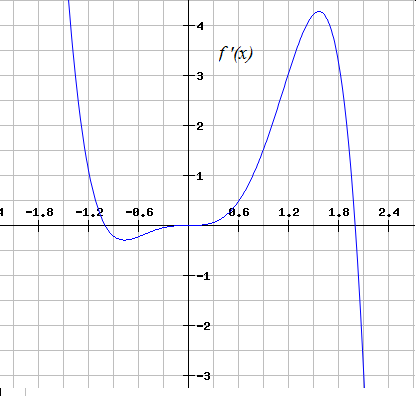
On which intervals is the following office increasing?

Correct respond:

Explanation:

The outset step is to find the first derivative.

Remember that the derivative of

Next, notice the disquisitional points, which are the points where  or undefined. To notice the  points, set the numerator to , to find the undefined points, set the denomintor to . The disquisitional points are and

The final footstep is to try points in all the regions  to encounter which range gives a positive value for .

If nosotros plugin in a number from the beginning range, i.e , we get a negative number.

From the second range,, we go a positive number.

From the third range, , we get a negative number.

From the last range, , we get a positive number.

And then the second and the last ranges are the ones where  is increasing.

Beneath is the complete graph of . On what interval(due south) is increasing?

Correct answer:

Explanation:

 is increasing when is positive (higher up the -axis). This occurs on the intervals.

Role A

Function B

Function C

Role D

Function E

v graphs of different functions are shown in a higher place. Which graph shows anincreasing/non-decreasing function?

Possible Answers:

Office D

Function Eastward

Function B

Role A

Office C

Correct reply:

Function E

Explanation:

A function is increasing if, for any, (i.eastward the gradient is always greater than or equal to zippo)

Office Eastward is the only function that has this property. Note that role E is increasing, but nonstrictly increasing

Detect the increasing intervals of the following function on the interval :

Correct answer:

Explanation:

To find the increasing intervals of a given office, 1 must decide the intervals where the role has a positivefirstderivative. To notice these intervals, showtime find the critical values, or the points at which the start derivative of the function is equal to zip.

For the given part,.

This derivative was found by using the power rule

.

When set equal to zippo,. Because we are just considering the open interval (0,5) for this function, nosotros tin ignore. Next, we look the intervals around the critical value, which are and . On the get-go interval, the offset derivative of the office is negative (plugging in values gives usa a negative number), which ways that the function is decreasing on this interval. Even so for the second interval, the first derivative is positive, which indicates that the function is increasing on this interval.

All Calculus one Resource

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the customs we tin can go on to improve our educational resources.

DMCA Complaint

If you lot believe that content available by ways of the Website (as divers in our Terms of Service) infringes i or more of your copyrights, please notify the states by providing a written notice ("Infringement Notice") containing the information described below to the designated amanuensis listed below. If Varsity Tutors takes activeness in response to an Infringement Notice, it will make a good organized religion attempt to contact the party that fabricated such content available by ways of the most recent email accost, if any, provided past such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that fabricated the content available or to third parties such as ChillingEffects.org.

Please be advised that you will exist liable for amercement (including costs and attorneys' fees) if you materially misrepresent that a production or activity is infringing your copyrights. Thus, if y'all are non sure content located on or linked-to by the Website infringes your copyright, you should consider commencement contacting an attorney.

Please follow these steps to file a notice:

You lot must include the following:

A concrete or electronic signature of the copyright owner or a person authorized to human action on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you lot claim to infringe your copyright, in \ sufficient detail to let Varsity Tutors to find and positively identify that content; for instance we crave a link to the specific question (not just the name of the question) that contains the content and a clarification of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your proper noun, address, telephone number and email address; and A statement by you: (a) that you lot believe in good faith that the use of the content that you claim to infringe your copyright is not authorized past constabulary, or by the copyright owner or such owner's agent; (b) that all of the information independent in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright possessor or a person authorized to human action on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form beneath:

Source: https://www.varsitytutors.com/calculus_1-help/how-to-find-increasing-intervals-by-graphing-functions

Posted by: francisoffined.blogspot.com

Share this post